Хотите ли увидеть и знать, как возникает и реализуется движение перигелия Меркурия и других планет Солнечной Системы? Увидеть движение перигелия можно в ситауции, которая была замоделирована при помощи компьютерной прграммы. Движутся модели двух объектов - планеты и Солнца. Объекты в моделированной ситуации ускоряют друг друга в соответствии с подобной математической функцией как та, которую Исаак Ньютон представил в законе всемирного тяготения.
Конечно, в моделированной ситуации нужно было применить другой масштаб расстояний между объектами и другой масштаб относительных ускорений и скоростей. Ибо то, что в природе изменяется в течение сотни лет и тысячелетия, представляется в виде пояснительного образа, который изменяется в течение нескольких, нескольких десятков секунд или минут.

Чтобы увидеть, как движется перигелий, нужно скопировать файл Merkury.zip (http://pinopa.narod.ru/Merkury.zip),*) в котором находятся две исполнительные программы exe и рабочие файлы gas. При помощи исполнительной программы надо открыть подходящий рабочий файл и включить течение процесса. В рабочем файле находяться закодированные начальные параметры процесса (орбитального движения планеты): расположение в системе координат и начальная скорость. А изменение движения объектов во время течения процесса, как было упомянуто выше, происходят на базисе их взаимного ускорения.

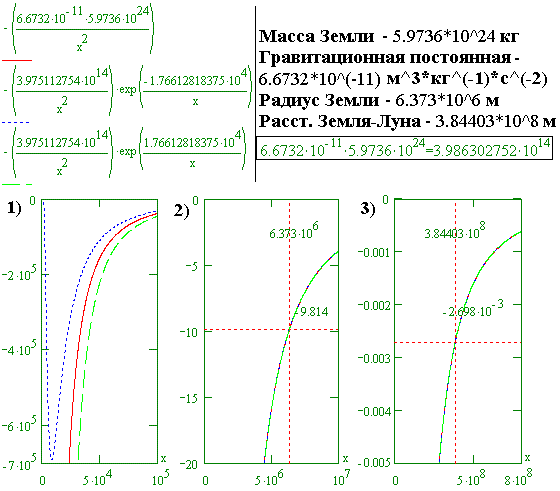
После включения процесса происходит движение объектов друг относительно друга и изменение скорости. А это ускорение происходит в соответствии с функцией Ньютона, в которой дополнительно существует экспоненциальный множитель. Чтобы приблизить суть явления, которое проявляет себя в виде движения перигелия Меркурия и других планет, ниже представлен пример, как изменяется гравитационное поле Земли. Ниже есть представлены три математические функции, которые описывают ускорения, изменяющиеся в соответствии с изменением расстояния, а также графики этих функций. Эти три функции отображают то, как небольшая есть разница ускорения, когда оно изменяется так, как это показал Ньютон, и когда оно изменяется немножко по-другому, ибо изменяясь дополнительно в соответствии с экспоненциальной функцией. На графиках 2) и 3) представлено течение этих фунций в двух масштабах. На одном графике видно течение функций с обозначеными радиусом Земли и гравитационным ускорением равным 9.814 м/с^2, а на втором графике видно течение функций с обозначеными средним значением расстояния Луны от Земли и гравитационным ускорением Земли (на этом расстоянии от Земли) равным 2.696*10^(-3) м/с^2. (В соответствии с принятым в физике соглашением на графиках ускорения есть отрицательны, что означает, что вектор ускорения направлен в сторону центра Земли.)

Первая функция известна со времен Ньютона. Две следующие функции возникают, когда в функции Ньютона положить экспоненциальный множитель в виде exp(-B/x) и в виде exp(B/x). (В этих двух функциях коэффициент B=1.76612818375, а измерением коэффициента B есть м, то есть, метр.)

Здесь стоит упомянуть, что коэффициент B=1.76612818375 и коэффициент пропорциональности 3.975112754*10^14 были отобраны по той причине, что они являются решением системы двух уравнений с двумя неизвестными. А параметры для этих уравнений добирались таким способом, чтобы графики этих функций перекрывались друг с другом в двух особенных точках, которые есть обозначены на графиках 2) и 3). Именно по этой причине коэффициент пропорциональности 3.975112754*10^14 отличается от произведения значений гравитационной постоянной G=6.6732*10^(-11) и массы Земли 5.9736*10^24. Эта разница свидетельствует о существовании некоторых ошибок, какие существуют в поданных параметрах Земли. А причиной ошибочных параметров может быть то, что либо автор статьи не знает точных значений этих параметров (и использовал не такие параметры, какие надо было использовать), либо эти ошибочные параметры существуют в физике, потому что их до сих пор точно не определили.

На графиках можно увидеть, что значащие различия в течении представленных функций существуют при малых расстояниях от начала координат. То есть, они существуют при таких расстояниях, при которых ни одна из трех перечисленных функций уже не отображает фактического гравитационного поля Земли, потому что эти расстояния меньше радиуса Земли. Но при больших расстояниях на графиках (в соответствующем масштабе) функции отличаются друг от друга столь мало, что это не заметно. Перечисленные изменения (различия) можно отнести до того, что происходит в природе.

А в природе, учитывая уже Солнечную систему и существующие большие расстояния планет от Солнца, экспоненциальный множитель почти не замечается, потому что он почти равен 1. Но фактически во время течения процесса (когда происходят изменения расстояния между планетой и Солнцем) этот множитель изменяется в соответствии с расстоянием х. В реальной ситуации расстояние планеты от Солнца очень большое, поэтому на этом расстоянии разница между этим множителем и 1 очень мала. По той причине влияние этого множителя в описании движения перигелия планеты тоже есть очень малое. Но в ситуациях, моделируемых при помощи компьютерной программы, экспоненциальный множитель в отношение своего значения не есть уже столь близкий к 1. По той причине в моделируемой ситуации можно наблюдать, как изменяется расположение перигелия и афелия движущейся планеты.

В компьютерной программе Gas2n.exe, в её источниковом коде, существует экспоненциальный множитель в виде exp(-B/x), а в программе Gas2n-Merkury.exe существует экспоненциальный множитель в виде exp(B/x). Этот экспоненциальный множитель при достаточно больших расстояниях х почти равен 1. Но в одном случае этот множитель немножко меньше 1, а во втором случае он немножко больше 1. Вследствие этой разницы в обоих исполнительных программах exe форма орбиты планеты изменяется различным образом.

От чувственного действия - видеть - до умственного действия - знать - существует относительно простой путь. Для этого достаточно анализирование фактов и соответствующие заключения. Можно опираться на закон всемирного тсготения, который подал Ньютон и соответствующим образом его корректировать. Это надо сделать именно таким способом, что дополнительно учитывается экспоненциальный множитель, который в теоретических исследованиях и заключениях был Ньютоном упущен.

Чтобы знать, нужно самому себе помочь и посмотреть. Астрономы могут некоторые опытные факты увидеть ментально, могут конфронтировать их друг с другом и на этой основе могут воображать, какой вид имеет розеточная траектория, по которой движется, например, Меркурий вокруг Солнца. Читатели этой статьи могут открыть программы Gas2n.exe и Gas2n-Merkury.exe, чтобы воображать движение Меркурия и увидеть его в другом масштабе на модели. На основе фактов, которые вытекают из астрономических наблюдений и измерений, астрономы принимают заключение, что движение перигелия происходит в то же направление, в которое планета кружит на орбите. Это означает, что во время между слудующими расположениями в точках перигелия планета выполняет оборот вокруг Солнца на угол, который немножко больше, чем 2*пи. По той причине орбита изменяется таким способом, как бы планета двигалась по траектории эллипса, который медленно вращается в то же навравление.
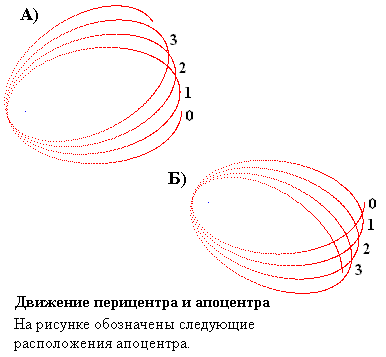
Конечно, направление движения перигелия свидетельствует о способе, по которому во время орбитального движения изменяется ускорение планеты.

Пользуясь программой Gas2n-Mekury.exe, можно наблюдать движение перигелия, которое подобно движению перигелия Меркурия (схема Б на представленном рисунке). А пользуясь программой Gas2n.exe, можно также наблюдать движение перигелия, которое идёт в противоположное направление, чем направление движения перигелия Меркурия.
Возможен ли этот второй вид движения и выступает ли он где-то в природе, в какой-то другой (чем наша) планетной системе? Возможно, что так. А как есть в действительности, это могут подтвердить только будущие исследования. Ибо существование такого движения перигелия зависит от того, возможно ли в природе возникновение такого результирующего гравитационного поля, которое ускоряло бы посторонние тела по такой ускорительной функции, которая в своей структуре содержала бы экспоненциальный множитель exp(-B/x), в котором В было бы положительным коэффициентом.
________________________________________

*) Внимание: Компьютерные моделируюшие программы, которые можно скачать на "страницы пинопы", работают правильно на компьютерах с системами Windows ME i Windows XP.

Богдан Шынкарык „Пинопа”
Польша, г. Легница, 2011.06.03.