Решение - выяснение - в некотором смысле существует уже от некоторого времени, но раньше оно не было сконфронтировано с проблемой, которая требовала выяснения. Этим решением - выяснением есть явление, которое связано с законом ничтожного действия, который описывается в статье «Закон ничтожного действия и связанные с ним явления». Только сопоставление двух явлений: явления в виде «увеличения массы тела» и явления в виде «ничтожного действия вешества», и их соединение логичными связями привело к возникновению пары – проблемы и её решения.

Явление «увеличения массы тела» вследствие (разгона тела до) всё большей скорости, называемое тоже явлением «релятивистической массы», известно с давних времен и оно уже имеет свою интерпретацию. Но фактически механизм течения явления до сих пор оставался тайной.

Когда механизм распознается, исчезает тайна... Оказывается, что так называемая релятивистическая масса может быть с равным успехом названа мнимой массой. Потому что в действительности в этом явлении никакое изменение массы не  происходит. То, что при увеличивающейся скорости всё труднее ускорять тело и прибавлять ему ещё больше скорости, не вытекает из увеличения массы. Это является следствием все меньшего времени пребывания тела в зоне, где действует ускорение. Это можно наблюдать на примере воздействия гравитационного поля Земли или моделируя явление, например, при помощи компьютерной программы ArtStand2.*

Сильное и ничтожное гравитационное воздействие Земли -
Место явления в природе

Разделение гравитационного воздействия Земли на ничтожное и сильное является относительным, но выполняет полезную роль.  Оно позволяет видеть отношения между физическими параметрами, какие существуют во время гравитационного воздействия в разных условиях. Это разделение связано с последствиями земного ускорения, возникающими в разных условиях.

Разделение воздействия на ничтожные и сильные можно рассматривать, учитывая два вида последствий. Последствиями воздействия есть изменение скорости ускоряемого тела и, связанное с этой скоростью, изменение кинетической энергии тела.

Принимая обозначения: g - гравитационное ускорение, S - длина дороги, по которой движется тело вследствие гравитационного ускорения, Vo - скорость тела в начале отрезка дороги S, V - конечная скорость тела после передвижени по дороге S, t - время движения тела на дороге S, можно вывести формулу на вычисление конечной скорости V. Вот последующие шаги вывода:
S=Vo*t+0.5*g*t^2 ;    0.5*g*t^2+Vo*t-S=0 ;    Del=Vo^2+2*g*S ;
t=(-Vo+(Vo^2+2*g*S)^0.5)/g ; (Решение t с отрицательным значением упущено.)
После подстановки времени t в известную формулу на  скорость получаем:
V=Vo+g*t=Vo+(-Vo+(Vo^2+2*g*S)^0.5)=(Vo^2+2*g*S)^0.5 .
Эту формулу на скорость можно перевести в вид V^2-Vo^2=2*g*S .

Выражение (V^2-Vo^2),  которое есть в уравнении V^2-Vo^2=2*g*S (и его правую часть тоже), можно назвать энергетическим показателем. Уравнение показывает, что вследствие воздействия того же гравитационного поля g (при предположении, что оно постоянно), на дороге одинаковой длины S, движущееся тело получает одинаковую порцию энергии, независимо от того, как большую скорость Vo оно имело в начале дороги S. Потому что значение энергетического показателя, его левая сторона в виде (V^2-Vo^2), умножена на половину массы движущегося тела (0.5*m), есть равна именно приращению кинетической энергии в гравитационном поле, а его правая сторона, в виде 2*g*S, умножена на половину массы движущегося тела (0.5*m), есть равна потенциальной энергии - и эта правая сторона уравнения имеет постоянное значение.

Во время движения тела в гравитационном поле происходит прирост скорости
DV=V-Vo=((Vo^2+2*g*S)^0.5)-Vo. Изменение прироста скорости в зависимости от скорости Vo[м/с], на дороге длиной 10 м, представлено на рис. DV(Vo).

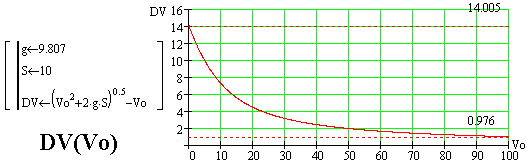
На графике видно, что самый большой прирост скорости (в точности он равен 14.005 м/с) имеет место тогда, когда тело ускоряется от начальной скорости равной ноль. Когда в очередних опытах начальная скорость Vo есть все больше, происходит быстрое уменьшение прироста скорости DV. При начальной скорости Vo=100 м/с прирост скорости тела равен лишь 0.976 м/с, то есть, после прохода по дороге длиной10 м скорость тела увеличивается только до значения 100.976 м/с.

Ниже находится "Замечание", которое касается изменений длины времени гравитационного воздействия на дороге S. Оно в подобной степени касается изменений прироста скорости DV. Потому что при больших скоростях Vo прирост скорости DV тоже есть (приблизительно) обратно пропорционален относительно скорости Vo. (Сравните формулы для вычисления DV и t.)

Именно здесь видны трудности, которые появляются, когда желаем разгонять тело до больших скоростей. А именно, когда тело ускоряется при малых скоростях движения, то виден отчетливый эффект в виде прироста скорости на той же дороге. При все больших скоростях движения тела (в очередних опытах) и при одних и тех же энергетических затратах этот эффект в виде прироста скорости на той же дороге быстро малеет. Это можно выяснить таким образом, что эффект есть все меньше, потому что тело все быстрее преодолевает тот сам участок дороги и более коротко находится под влиянием действующего на этой дороге ускорения g.

Функция длины времени, за которое тело ускоряется на дороге S, в зависимости от его начальной скорости Vo, представляет рис. t(Vo).

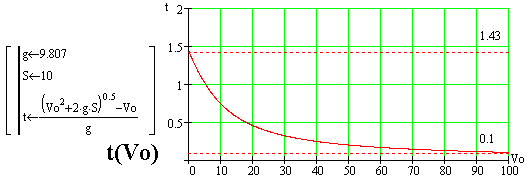
На графике видно, что когда движение тела (частицы) начинается от скорости равной ноль, то воздействие на дороге S длится наидольше (в точности оно длится 1.43 с). Зато в очередних опытах, когда начальная скорость Vo все больше, время воздействия на той же дороге быстро уменьшается. При начальной скорости Vo=100 м/с ускорение тела длится уже только 0.1 с. При ещё больших скоростях Vo время воздействия изменяется приблизительно обратно пропорционально значению Vo, то есть, например, при стократно большей начальной скорости Vo время воздействия будет стократно короче.

Замечание: Если смотреть на математическую структуру формулы t(Vo)=(-Vo+(Vo^2+2*g*S)^0.5)/g, обратно пропорциональная зависимость (она только приблизительная) на первый взгляд не видна. О существовании этой зависимости можно убедиться лишь после подстановки конкретных чисел. Итак, пример А - при скорости Vo=100 м/с время t=0.1 с. Зато - пример Б - при скорости Vo= 10 000 м/с (то есть, при скорости в 100 раз больше, чем в примере А) время t=10^(-3) с (то есть, время t в 100 раз короче, чем в примере А).

Появляющиеся трудности, которые связаны с разгоном тел (частиц) до все большей скорости, хорошо видны в работе акселераторов. Чтобы получить значительные приросты скоростей, также в пределе больших скоростей тел (частиц), единственным выходом есть увеличение энергетических затрат на их ускорение. В применяемой здесь конвенции, какая была принята для иллюстрирования явления, это равнозначно с увеличением значения ускорения g. Здесь предполагается, что увеличение дороги S, на которой происходит действие ускорения, не входит в план, потому что, например, разработка и реализация многократно большего и дорогостоящего акселератора не предвидывается.
Ускорение в акселераторе это дело техники, поэтому ниже оно будет обозначаться как Ge.

Если было бы нужно, чтобы акселератор, назависимо от начальной скорости частиц, прибавлял им на дороге S постоянный прирост скорости, то он должен создавать ускорение Ge, которое изменялось бы в зависимости от Vo по некоторой функции. Принимая, например, что разница скоростей D=4м/с, эта функция будет иметь вид как на рисунке Ge(Vo).


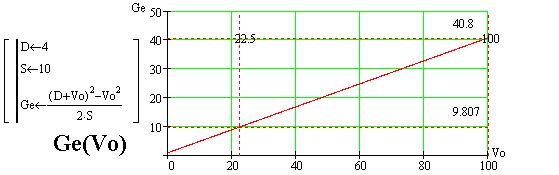
Такой акселератор ускорял бы частицы с ускорением Ge=9.807, если в начале процесса ускорения они обладали бы скоростью 22.5175 м/с. Тогда на конец процесса ускорения частицы обладали бы скоростью 26.5175 м/с. Либо действовал бы на частицы с ускорением Ge=40.8, если в начале процесса ускорения они обладали бы скоростью 100 м/с. А тогда на конец процесса ускорения частицы обладали бы скоростью 104 м/с.

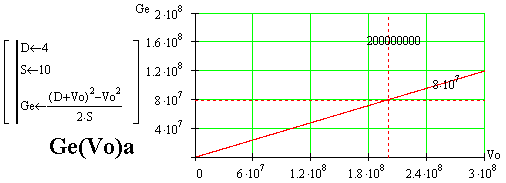
А какое значение Ge было бы необходимо, если бы прирост скорости 4 м/с должен получиться на акселераторе при начальной скорости частиц равной 200000 км/с, то есть, 2*10^8 м/с? После подстановки в формулу Ge=(((D+Vo)^2)-Vo^2)/(2*S) значений: D=4 м/с, S=10 м, Vo=2*10^8 м/с, и вычисления выходит, что Ge=8*10^7 м/с^2. Это есть необычно большое значение ускорения... а на дороге длиной S=10 м частицы ускорились бы лишь до скорости 200000004 м/с.

Но если было бы возможно построение акселератора, который придавал бы такое ускорение и оно действовало бы постоянно, тогда ускорение частиц от нолевой скорости до скорости 2*10^8 м/с длилось бы t=V/Ge=(2*10^8)/(8*10^7)=2.5 с. А длина дороги, на которой такое ускорение должно действовать, должна равняться не 10 м, но S=0.5*Ge*t^2=2.5*10^8 м,  то есть, 250 тыс. км.

Заключение
На основе перечисленных здесь примеров можно выводить заключения о свойствах поля, которое является причиной ускорения частиц, а также о других физических условиях, какие существуют во время ускорения. А в особенности, можно вывести заключения о более сильном или более слабом влиянии поля на вещество (а точнее, влиянии поля на поле) в зависимости от скорости, с которой оно движется. Такие заключения были уже приняты раньше на основе моделирования полевых явлений при помощи моделирующей компьютерной программы - они были описаны в статье «Закон ничтожного действия и связанные с ним явления».

Следует иметь ввиду, что выше представленные зависимости не описывают физической природы вещества, а только показывают математические отношения между числами. В особенности, речь идёт об отношениях между числами, когда они связаны друг с другом по формуле (энергетическом показателе) V^2-Vo^2=2*g*S. Это из математической природы чисел следует, что при больших значениях двух чисел (V i Vo), когда разница их квадратов имеет принятое постоянное значение, получается такое, что разница этих чисел есть малая. Здесь эти числа аккурат касаются скорости и возникающие соотношения есть пригодны для описания скорости вещества, когда оно ускоряется. Но это не формулы решают о поведении вещества - причиной всего есть само вещество, есть его природа. Следовательно, только большое количество проведенных физических опытов и сравнение друг с другом результатов опытов  и результатов математического описания (такого как выше) позволит оценивать, соответствует ли это описание реальной действительности и правильно ли её отображает.

Сейчас физики-теоретики, поклонники гения А. Эйнштейна, думают, что обе теории относительности правильно описывают мир и протекающие в нём явления. Они не учитывают описываемых здесь математических зависимостей, потому что они их не знают. Они думают, что одновременно с увеличением скорости тела увеличивается его масса. Теперь они должны задуматься, каким образом стать учитывать в своих мнениях быстро малеющий прирост скорости при разгоне тела до все большей скорости, который (то быстро малеющий прирост скорости) не является следствием увеличения массы тела, но он попросту является следствием самого увеличения скорости тела.

Время жизни короткоживущих частиц зависит от физических параметров их составных элементов. Но оно также зависит от влияний, которые доходят до структуры частицы из окружающей среды. Увеличивающаяся скорость частиц значительно сокращает время их воздействия  со средой, то есть, сокращает время их влияния на среду и влияния среды на эти частицы, а поэтому также уменьшает отрицательные следствия этих влияний. Следовательно, увеличивающаяся скорость частиц значительным образом влияет на увеличение времени их жизни.
В этом случае поклонники теорий относительности также должны задуматься...
Это позволит им увидеть реальность явления, которое заключается в увеличении времени жизни частиц. Но это явление не имеет ничего общего с изменением протекающего времени как физического параметра.

Написал: Богдан Шынкарык "Пинопа"
Польша, г. Легница, 4.11.2009 г.
__________________
*) В случае появления трудностей, связанных с моделированием гравитационных процессов при помощи компьютерной программы ArtStand2, пишите на э-адрес: pinopa@yandex.ru. Описание трудностей и способ их устранения буду выкладывать ниже.

Ускорение электрона, ускорение автомобиля - Мощность Р

Имея формулы на ускорение Ge=(((D+Vo)^2)-Vo^2)/(2*S), время t=(-Vo+(Vo^2+2*Ge*S)^0.5)/Ge и применяя обозначения, которые использовались в выше приведенной статье, можно вывести зависимость для вычисления мощности, которая нужна для ускорения массы m. Вот очередние шаги вывода:
Энергия, используемая для ускорения массы m на дороге S,  En=m*Ge*S.
Мощность P=En/t=m*S*(Ge^2)/(-Vo+(Vo^2+2*Ge*S)^0.5)=m*S*(Ge^2)*(Vo+(Vo^2+2*Ge*S)^0.5)/2*S*Ge;
P=0.5*m*Ge*(Vo+(Vo^2+2*Ge*S)^0.5)=0.5*m*Ge*(Vo+(Vo^2+((D+Vo)^2)-Vo^2)^0.5)=0.5*m*Ge*(2*Vo+D);
P=0.5*m*(2*Vo+D)*(((D+Vo)^2)-Vo^2)/(2*S)=m*D*((2*Vo+D)^2)/(4*S).

На ниже приведенном рисунке представлен график мощности P(Vo) (в ватах) в зависимости от начальной скорости Vo. График иллюстрирует случай ускорения электрона - его масса m=9.10938*10^(-31) кг.

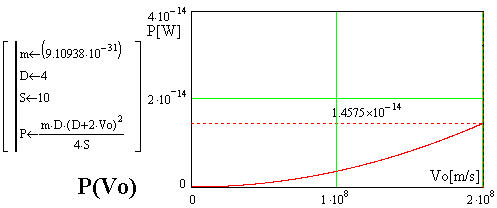
На графике видать, что при начальной скорости электрона Vo= 2*10^8 м/с для выработки требуемого ускорения (увеличения скорости на 4 м/с на дороге 10 м) необходима мощность P=1.4575*10^(-14) Вт.
В таком случае как очень большое значение скорости Vo электрона, так и очень малая мощность, которая нужна для ускорения электрона, так чтобы на дороге 10 м его скорость увеличилась до значения  4 м/с, слабо сочетаются с ежедневным опытом каждого человека. Значительно легче воображать трудности, возникающие при ускорении , например, гоночного автомобиля массой 1000 кг. Рисунок P(Vo)a представляет график мощности, которая есть необходима для ускорения такого автомобиля в пределе значений начальной скорости Vo от 0 до 100 м/с, так чтобы на дороге длиной 10 м его скорость увеличилась на 4 м/с.

 

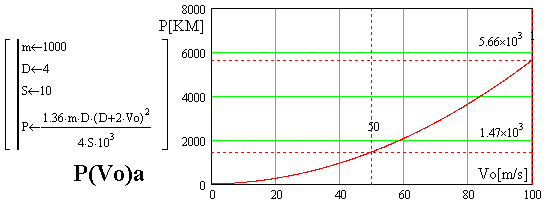
На графике можно прочитать, что для ускорения автомобиля, когда он мчится со скоростью 50 м/с (180 км/ч), так чтобы на дороге длиной 10 м он ускорился до скорости 54 м/с, необходима мощность двигателя P=1470 л.с. (на рис. обозначена как KM - Механический Конь). Это есть мощность, которая необходима только для ускорения, а кроме этого двигатель автомобиля должен обладать надбавкой мощности для преодоления всякого сопротивления трения в механизмах машины и сопротивления воздуха.

Надо здесь обратить внимание на то, что мощность P=1470 л.с. это временная мощность, которая необходимо нужна в момент, когда автомобиль мчится со скоростью Vo=50 м/с. Ибо когда автомобиль ускорится, а его скорость увеличится, то вследствие этого также увеличится временная мощность, которая для этой новой скорости должна быть больше.

Для обеспечения подобного вида эффективности при ускорении этого автомобиля, но в ситуации когда он имеет скорость Vo=100 м/с, нужна уже мощность двигателя, которая значительно больше. При этой начальной скорости двигатель должен иметь мощность P=5660 л.с.

Как видать, масса ускоряемого автомобиля постоянно остаётся одной и той же. Но при увеличивающейся скорости Vo, для ускорения автомобиля, чтобы он получил ещё больше скорости, необходимо прикладывать к нему всё больше энергии в более короткое время. То есть, говоря по-другому, главной причиной ограничения скорости движения тела (автомобиля) не есть сопротивление трения. (Можно вообразить ситуацию, в которой непрестанно ускоряемая ракета летит в вакууме, где нет трения.) Главной причиной является то, что для получения все большей скорости надо непрестанно прибавлять в тело все больше энергии.

Это количество прибавляемой энергии увеличивается пропорционально квадрату скорости - оно увеличивается подобным образом, как необходимая для движения мощность двигателя. Если этого большого прироста энергии (прибавляемой в тело) не будет, а вместо этого, например, она будет постоянно оставаться на одном и том же уровне, то приросты скорости тела (при постоянно увеличивающейся его скорости) будут всё меньше и они будут приближаться к нулю. Зато скорость тела будет приближаться до некоторого квази-постоянного (почти постоянного) граничного значения, которое будет зависеть от величины дозы прибавляемой энергии. То есть, даже в вакууме скорость тела будет подлежать ограничению, несмотря на то, что там не существует сопротивление трения. (Но, конечно, бесконечно длительное прибавление в тело энергии будет следствовать его бесконечной скоростью! - Только кто это выдержит?)

Эта ситуация хорошо видна, если для анализа использовать уравнение - энергетический показатель: V^2-Vo^2=2*Ge*S. После деления обоих сторон уравнения на (V+Vo) выходит, что разница скорости (или прирост скорости)  V-Vo=2*Ge*S/(V+Vo).

Во время постоянного прибавления в тело даже небольшого количества энергии в единицу времени его скорость увеличивается неограничено. Но приросты скорости приближаются к нулю. Следовательно, можно предполагать, что скорость есть квази-постоянной тогда, если только прирост скорости есть меньше от некоторой принятой очень малой величины. Потому что тогда прирост скорости происходит так медленно, что изменение скорости очень трудно замечается.

Итак, например, если принять, что энергетический показатель 2*Ge*S=10^3[(м/с)^2], а прирост скорости V-Vo=2*Ge*S/(V+Vo)=<10^(-3)[м/с], тогда можно приблизительно вычислить , что квази-постоянна скорость Vqs=>2*Ge*S/(2*10^(-3))=10^6[м/с]. То есть, для такого случая постоянного прибавления энергии (одной и той же дозы в течение 1 с) и ускорения тела, когда энергетический показатель равен 10^3[(м/с)^2], его квази-постоянна скорость Vqs будет равняться 1000 км/с. При этой скорости последующее ускорение тела, при действии на него той же мощности, сопровождается увеличением скорости на около 1 мм/с на дороге, которую это тело преодолевает в течение 1 с, то есть, на дороге 1000 км.

Чтобы приобрести мнение на тему того, как выглядит эта ситуация в энергетическом отношении, можно предположить, что в выше приведенном примере ускоряется тело массой 1 кг. В таком случае прибавляемая энергия (в течение 1 с) En=m*Ge*S=0.5*10^3[дж], а необходимая мощность P=0.5[кВт]. Если на подобном принципе в тело будет прибавляться n-кратно больше энергии, то его квази-постоянная скорость Vqs будет n-кратно больше.

Написал: Пинопа
Польша, г. Легница, 10.11.2009 г.