Конструктивная теория поля
- коротко и шаг за шагом
Содержание
1. Галилей - гравитационный закон свободного падения
2. Иоганн Кеплер - третий закон движения планет
3. Исаак Ньютон - законы динамики и закон всемирного тяготения
4. Пинопа создает Конструктивную теорию поля. Пинопа открывает...
А) Вневременной характер гравитационного воздействия
Б) Тождественность воздействий фундаментального и гравитационного
В) Фундаментальная частица вещества
Г) Двоякий, зависимый от расстояния, характер фундаментального воздействия
Д) Абсолютное и относительное взаимное проницание компонентов вещества
Е) Принцип минимализации потенциалов пространства
Ж) Динамика самодейственного движения вещества
З) Самодейственное движение вещества в свете опытных фактов
1. Галилей - гравитационный закон свободного падения
Галилео Галилей (1564 - 1642) ведёт опыты с гравитацией. Он сбрасывает
с большой высоты предметы и измеряет время их падения. На основе полученных
результатов он делает выводы, которые мы сегодня знаем в виде закона свободного
падения тел в гравитационном поле. Этот гравитационный закон Галилея гласит,
что тела независимо от величины их массы падают в гравитационном поле с
одинаковыми ускорениями. По-другому говоря, гравитационное поле трактует
эти тела одинаковым способом и одинаково их ускоряет.
2. Иоганн Кеплер - третий закон движения планет
Иоганн Кеплер (1571 - 1630) анализирует результаты астрономических
наблюдений своего учителя Тихо Браге и формулирует три закона движения
планет. Часть аналитических выводов сегодня известна как третий закон Кеплера.
Этот закон гласит, что отношение квадрата периода обращения планеты вокруг
Солнца к кубу большой полуоси её эллиптической орбиты (то есть, среднего
расстояния от Солнца) имеет постоянную величину для всех планет Солнечной
Системы. Или иначе говоря, квадраты периодов обращения планет вокруг Солнца
есть пропорциональны кубам больших полуосей.
Это можно записать при помощи формулы: 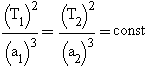 ,
где T с индексом 1 или 2 это периоды обращения двух планет, зато а с индексом
1 или 2 это большие полуоси этих орбит. Эту формулу можно немножко изменить
и для двух планет написать её в виде
,
где T с индексом 1 или 2 это периоды обращения двух планет, зато а с индексом
1 или 2 это большие полуоси этих орбит. Эту формулу можно немножко изменить
и для двух планет написать её в виде 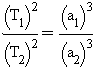 .
Можно ещё перейти к более идеализированной форме планетной системы, в которой
планеты движутся по круговым орбитам. Тогда в формуле вместо отношения
кубов больших полуосей эллиптических орбит выступает отношение кубов радиусов
круговых орбит, а формула имеет вид
.
Можно ещё перейти к более идеализированной форме планетной системы, в которой
планеты движутся по круговым орбитам. Тогда в формуле вместо отношения
кубов больших полуосей эллиптических орбит выступает отношение кубов радиусов
круговых орбит, а формула имеет вид 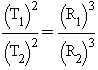 .
.
Характер структуры формулы, а заодно характер третьего закона Кеплера,
есть кинематический. Это значит, что закон Кеплера и формула описывают
движение на эллиптической или круговой орбите при использовании параметров
орбиты и времени движения, а не учитываются причины такого вида движения.
В этом отношении ситуация есть подобна, как при описании ускорения тела
на круговой орбите. В этом случае центростремительное ускорение описывается
на основе скорости тела на орбите и радиуса орбиты.Формула для центростремительного
ускорения имеет вид: 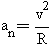 ,
а её обоснование показывает ниже приведенный пример.
,
а её обоснование показывает ниже приведенный пример.
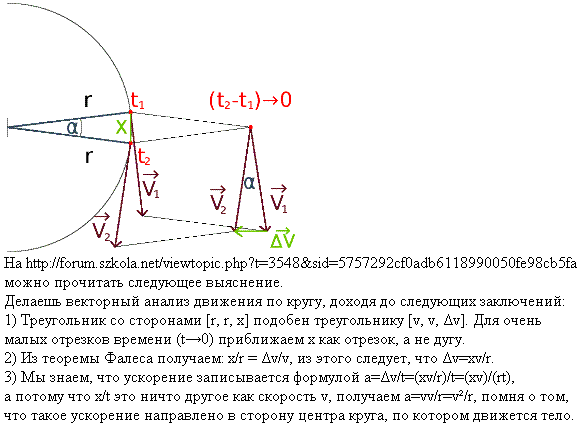 Какое есть отношение друг к другу этих двух зависимостей, касающейся третьего
закона Кеплера и касающейся центростремительного ускорения, будет пояснено
позже.
Какое есть отношение друг к другу этих двух зависимостей, касающейся третьего
закона Кеплера и касающейся центростремительного ускорения, будет пояснено
позже.
3. Исаак Ньютон - законы динамики и закон всемирного тяготения
Исаак Ньютон (1643 - 1727) занимается математическим анализом - разрабатывает
диференциальное и интегральное исчисление - в то время он также анализирует
поведение тел в гравитационном поле и в процессе орбитального движения.
Сегодня, когда мы знаем результаты аналитической работы Ньютона в виде
трех законов динамики и закона всемирного тяготения, мы можем также увидеть,
что (и каким способом) он пользовался научными достижениями Галилея и Кеплера.
Гравитационный закон Галилея, который касается свободного падения тел в
гравитационном поле, хотя это не видно на первый взгляд, содержится в законе
всемирного тяготения и в третьем законе динамики. Закон Галилея, говоря
об одинаковом ускорении в гравитационном поле, в подтексте говорит о том,
что величина ускорения зависит только от массы тела, в гравитационном поле
которого происходит это ускорение. И это именно можно уже четко увидеть,
анализируя зависимости между параметрами движения двух тел в какой-нибудь
примерной планетной системе. Вот как выглядит эта ситуация.
Опираясь на закон всемирного тяготения, мы можем рассмотреть ситуацию
двух тел, тяжелого тела массой М и легкого тела массой m, которые движутся
по круговым орбитам вокруг общего центра тяжести. Эти тела образуют стабильную
планетную систему благодаря взаимному ускорению. В этой системе тела взаимодействуют
друг на друга при помощи сил, которые равны по величине и имеют противоположные
направления. Учитывая, что каждая из этих сил является произведением массы
тела, на которое влияет ускоряющее действие соседа, и этого ускорения,
равенство этих сил существует именно по той причине, что ускорение зависит
(пропорционально) только от этого соседа. Если зависимость (математическая
формула), которая описывает ускорение, обладала бы другим характером, то
не существовало бы равенство сил и в таком случае не работал бы третий
закон динамики Ньютона.
Зная результаты исследований Галилея над гравитацией, Ньютон размышлял
о том, как с увеличением расстояния измененяется гравитация небесных тел,
а в частности, как измененяется гравитация Земли. Несомненно, он знал зависимость,
которая связана с движением тел по окружности, которую сегодня изучают
лицеисты. Итак, он знал о существовании зависимости, описывающей центростремительное
ускорение и знал о превращении этой зависимости (формулы), которое сегодня
записывается при помощи формул как 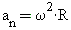 и
и 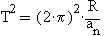 . Из последней
зависимости следует, что если гравитационное ускорение не изменялось бы
при увеличении расстояния, то есть, центростремительное ускорение не зависело
бы от радиуса орбиты, то скорость тела на орбите должна быть такой, что
квадрат периода обращения тела на орбите был бы пропорционален радиусу
орбиты. По-другому говоря, тогда должно быть так, что
. Из последней
зависимости следует, что если гравитационное ускорение не изменялось бы
при увеличении расстояния, то есть, центростремительное ускорение не зависело
бы от радиуса орбиты, то скорость тела на орбите должна быть такой, что
квадрат периода обращения тела на орбите был бы пропорционален радиусу
орбиты. По-другому говоря, тогда должно быть так, что 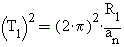 ,
, 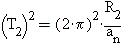 ,
и следовательно, правильной должна быть зависимость
,
и следовательно, правильной должна быть зависимость 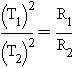 .
.
Следует подчеркнуть, что именно так было бы тогда, если гравитационное
ускорение, происходящее от данного небесного тела, при изменении расстояния
(от него) оставалось бы неизменным. Но Ньютон также знал об исследованиях
Кеплера и знал о том, что третий закон Кеплера имеет вид 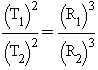 .
Исходя из этого, Ньютон сделал вывод, что центростремительное ускорение,
которое действует на тело на орбите, которое является причиной искривления
траектории движения и её круговой формы, должно быть обратно пропорционально
квадрату радиуса орбиты (расстоянию). По-другому говоря, Ньютон сделал
вывод, что ускорение силы тяжести должно изменяться (по сегодняшней записи)
в соответствии с формулой
.
Исходя из этого, Ньютон сделал вывод, что центростремительное ускорение,
которое действует на тело на орбите, которое является причиной искривления
траектории движения и её круговой формы, должно быть обратно пропорционально
квадрату радиуса орбиты (расстоянию). По-другому говоря, Ньютон сделал
вывод, что ускорение силы тяжести должно изменяться (по сегодняшней записи)
в соответствии с формулой 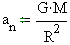 .
Потому что только тогда будет так, что
.
Потому что только тогда будет так, что 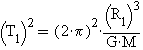 ,
, 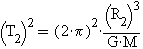 ,
а также
,
а также 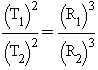 ,
то есть, только тогда это будет в соответствии с третьим законом Кеплера
.
,
то есть, только тогда это будет в соответствии с третьим законом Кеплера
.
Используемое сегодня в физике понятие гравитационного поля выражено
достаточно отчётливо. Но не всегда так бывало и только немногие знают,
каким образом это понятие возникало и что фактически оно значит. Сегодня
можно догадываться, что развитие значения этого понятия началось вследствие
аналитических исследований Ньютона. Первым шагом и канвой для появления
понятия поля, которое окружает данное тело, были результаты анализа распределения
ускорений посторонних тел, которые эти посторонние тела приобретают в результате
влияния данного тела. В связи с небесным телом появился пространственный
образ распределения ускорений, который то образ обладал центрально-симметричным
характером.
Неизвестно, был ли это Ньютон, или кто-либо другой, но, несомнено,
это был человек, который уже владел дифференциальным и интегральным исчислением.
Этот знаток математического анализа нашёл интегральную функцию, которая
была связана с функцией распределения ускорений вокруг небесного тела -
она возникла вследствие интегрирования функции, описывающей распределение
ускорений. Чтобы при помощи слов можно было описать как целое теоретические
зависимости, какие возникли таким способом, были созданы понятия поля,
потенциала поля, напряжённости поля. При том, в численном отношении и в
отношении описания при помощи математической функции, напряжённость поля
была тождественна с пространственным распределением ускорений.
Такие были начала описания гравитационного воздействия, но тоже начала
досконального описания свойств и строения вещества как основы конструктивной
теории поля.
4. Пинопа создает Конструктивную теорию поля. Пинопа открывает...
Пинопа (род. 1944 г.) занимается аналитическим исследованием зависимостей
между разновидными физическими явлениями. Открытия Пинопы и интерпретации
физических явлений можно представить следующим образом:
А) Вневременной характер гравитационного воздействия
Процесс гравитационного воздействия между объектами происходит без
участия времени. Это есть процесс, который происходит непосредственно по
месту нахождения объекта, а ускорение объекта происходит в соответствии
с законом всемирного тяготения и в соответствии с распределением других
объектов в пространстве. Потому что способ ускорения есть уже закодирован
во всем пространстве в гравитационном поле, которое окружает каждый объект.
Поэтому каждый объект, который находится в этом поле (сформированном всеми
соседними объектами) ускоряется сразу в соответствии с результирующей напряжённостью
поля. Эта результирующая напряжённость поля зависит от расположения в пространстве
других (остальных) объектов и от их физических параметров.
Другие способы объяснения механизма гравитационного воздействия - а
именно, что оно происходит при посредстве волн или что оно происходит при
посредстве обмена посредственными частицами, который то обмен реализуется
объектами - не соответствуют опытным фактам. Потому что факты свидетельствуют
о немедленном изменении величины гравитационного ускорения, а именно, что
это изменение происходит тотчас же, как только изменяется расстояние между
объектами.
Таким подтверждающим фактом может служить движение компонентов двойной
звезды PSR B1913 +16. Расстояния между компонентами этой двойной системы
и траектория движения есть такие, что в периастре, когда между ними минимальное
расстояние, свет это расстояние проходит в течение ок. 2,5 секунд, а в
апоастре, когда между ними максимальное расстояние, свет это расстояние
проходит в течение ок. 10,5 секунд. Скорость пульсара на „почти” эллиптической
орбите в этой системе меняется от 450 км/с до 110 км/с. (Одно полное вращение
на орбите длится ок. 7,752 часа.) При таких скоростях элементы двойной
системы в течение времени 2,5 секунд (или в 10,5 секунд) преодолевают огромные
расстояния, искривляя при этом соответсвующим образом свои траектории.
Такое поведение компонентов двойной звезды PSR B1913 +16 возможно только
в таком случае, когда гравитационное воздействие имеет вневременный характер.
Б) Тождественность воздействий фундаментального и гравитационного
Гравитационное воздействие тождественно с фундаментальным воздействием,
которое происходит между фундаментальными элементами вещества, а гравитационное
поле тождественно с фундаментальным полем. Гравитационное поле тела является
результирующим полем, которое возникает вследствие наложения друг на друга
гравитационных полей всех компонентов этого тела. То же самое фундаментальное
воздействие, которое при больших расстояниях проявляется в виде хорошо
известного результирующего гравитационного воздействия, при малых расстояниях
является тем же воздействием, которое соединяет компоненты (элементы) в
сложные структурные системы и является основой всех физических явлений,
которые в этом масштабе происходят в веществе.
Фундаментальные воздействия при малых расстояниях между компонентами,
при которых происходит формирование материальных структур, это те же самые
воздействия, которые теперь известны как сильные и слабые ядерные воздействия,
межатомные воздействия и другие. А воздействия между структурами в более
сложной форме есть известны, например, как электрические воздействия между
проводниками с током, магнитные воздействия и электростатические воздействия.
В) Фундаментальная частица вещества
Центрально-симметричное фундаментальное поле тождественно с фундаментальной
частицей вещества. Из таких фундаментальных частиц, на основе того же самого
принципа взаимодействия, который работает при гравитационных воздействиях,
спонтанно образуются стабильные структуры вещества. Различное поведение
фундаментальных частиц на больших расстояниях и на малых расстояниях вытекает
из природы вещества, которая может быть описана при помощи математических
функций. А более конкретно, при помощи функций можно описать характер
напряжённости фундаментального поля. Этот характер изменений фундаментального
поля делает возможным то, что при мега-расстояниях могут образовываться
стабильные системы в виде планетных систем, для чего необходимо орбитальное
движение, а при нано-и микро-расстояниях, образуятся устойчивые структуру
в виде атомов, малых и больших молекул, кристаллов и т.п., для которых
орбитальное движение является излишним.
При мега-расстояниях воздействие между отдельными частицами - центрально-симметричными
поля - и воздействие между всякими сложными структурными системами, например,
между Солнцем и кружащими вокруг него планетами, есть такое, что всегда
проявляется в виде стремления приблизить эти объекты друг к другу. Эти
объекты всегда ускоряют другие объекты в свою сторону, а это ускорение
достаточно точно описывает формула из гравитационного закона Ньютона 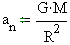 .
А при нано-расстояниях фундаментальные частицы - то есть, ц.с. поля - в
зависимости от расстояния до центральной точки могут в этих областях ускорять
другие подобные частицы (ц.с. поля) в направление "к центру" этого поля,
тогда можно говорить о притяжении, или - находясь на немножко другом расстоянии
- могут их ускорять в противоположное направление, а тогда можно говорить
об отталкивании этих частиц. Такое воздействие фундаментальных частиц,
а также воздействие атомов и молекул, которое имитирует притяжение и отталкивание
других подобных частиц в области небольших расстояний от их центральных
районов, связано с существованием соответствующего распределения потенциалов
поля. Описанное поведение фундаментальных частиц, атомов и молекул, подтверждается
экспериментальными фактами. Это подтверждается существованием стабильной
структуры вещества, кристаллов, атомов. Такое поведение вытекает по просту
из существования способности составляющих элементов вещества создавать
стабильные структурные системы. А эти способности являются следствием подходящего
распределения потенциала в структурных компонентах, что и приводит к таким
последствиям. Можно сказать более конкретно, что такие свойства являются
результатом существования сферических потенциальных оболочек в ц.с. полях,
которые концентрически окружают центральные точки.
.
А при нано-расстояниях фундаментальные частицы - то есть, ц.с. поля - в
зависимости от расстояния до центральной точки могут в этих областях ускорять
другие подобные частицы (ц.с. поля) в направление "к центру" этого поля,
тогда можно говорить о притяжении, или - находясь на немножко другом расстоянии
- могут их ускорять в противоположное направление, а тогда можно говорить
об отталкивании этих частиц. Такое воздействие фундаментальных частиц,
а также воздействие атомов и молекул, которое имитирует притяжение и отталкивание
других подобных частиц в области небольших расстояний от их центральных
районов, связано с существованием соответствующего распределения потенциалов
поля. Описанное поведение фундаментальных частиц, атомов и молекул, подтверждается
экспериментальными фактами. Это подтверждается существованием стабильной
структуры вещества, кристаллов, атомов. Такое поведение вытекает по просту
из существования способности составляющих элементов вещества создавать
стабильные структурные системы. А эти способности являются следствием подходящего
распределения потенциала в структурных компонентах, что и приводит к таким
последствиям. Можно сказать более конкретно, что такие свойства являются
результатом существования сферических потенциальных оболочек в ц.с. полях,
которые концентрически окружают центральные точки.
Г) Двоякий, зависимый от расстояния, характер фундаментального воздействия
Разные способы воздействия фундаментальных частиц и всяких построенных
из них сложных структурных систем при нано-расстояниях и при мега-расстояниях
можно показать при помощи соответствующих математических функций. Существенными
являются результаты физических исследований и именно к этим результатам
должны подбираться подходящие функции. Известно, что при мега-расстояниях
гравитационное воздействие не изменяется точно так, как это представил
Ньютон. Ибо если оно при изменении расстояния изменялось бы точно в соответствии
с законом Ньютона, тогда орбиты планет в Солнечной Системе имели бы точную
форму эллипса. А такой формы они не имеют. Найболее отчётливым примером
есть явление, которое известно как движение перигелия Меркурия. Движение
перигелия Меркурия происходит медленно, ибо его величина равна 42,98 угловых
секунд в столетие. Но движение перигелия Меркурия свидетельствует о том,
что фактическая орбита этой планеты имеет розеточную форму. Изменчивость
орбиты Меркурия можно описать более точно, если к функции Ньютона дописать
экспоненциальный фактор. Тогда изменчивость гравитационного ускорения описывалась
бы при помощи функции в виде 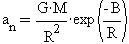 .
Для анализа движения лучше пользоваться той же функцией, но записанной
как напряжённость поля, которая изменяется в зависимости от расстояния
R. Её можно также записать добавляя отрицательный знак, который рекомендуется
здесь для того, чтобы функция потенциального поля была положительной. Тогда
функция напряжённости поля вдоль любого луча, который выходит из центральной
точки поля, имеет вид
.
Для анализа движения лучше пользоваться той же функцией, но записанной
как напряжённость поля, которая изменяется в зависимости от расстояния
R. Её можно также записать добавляя отрицательный знак, который рекомендуется
здесь для того, чтобы функция потенциального поля была положительной. Тогда
функция напряжённости поля вдоль любого луча, который выходит из центральной
точки поля, имеет вид 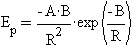 ,
а потенциал такого поля описывает экспоненциальная функция, то есть, функция
Е, в виде
,
а потенциал такого поля описывает экспоненциальная функция, то есть, функция
Е, в виде 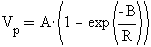 . В этих
формулах А есть коэффициентом пропорциональности, а В экспоненциальным
коэффициентом.
. В этих
формулах А есть коэффициентом пропорциональности, а В экспоненциальным
коэффициентом.
Ниже представлены диаграммы, на которых показан примерный потенциал
поля (функция Е) и напряженность поля.
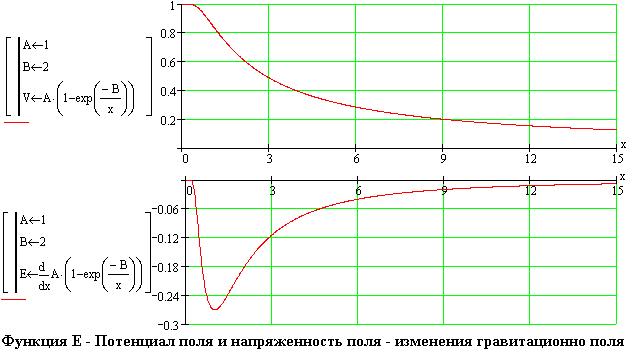
Запись распределения поля в пространстве с помощью функции E и коэффициентов
А и В имеет то преимущество, что позволяет объединить (унифицировать) всякие
воздействия. Такая запись помогает свести все известные воздействия к одной
общей причине их существования и проявления - этой общей причиной является
взаимодействие между фундаментальными элементами вещества. Но эта запись
также помогает разъединить понятие гравитационного взаимодействия небесных
тел, которое существует со времен Ньютона, и увидеть индивидуальный характер
гравитационного поля любого небесного тела. Этот индивидуальный характер
гравитационного поля небесных тел выражается главным образом в том, что
существует движение перигелия планет и звезд. В случае Меркурия и других
планет Солнечной системы величина
движения перигелия измеряется не более десятками угловых секунд в столетие.
Но в случае компонентов двойной звезды PSR B1913 +16 перигелий их орбит
вращается со скоростью 4,2 угловых градусов в год. Логичное описание такого
движения стало возможным благодаря использованию функции Е.
При нано-расстояниях, на которых есть потенциальные оболочки, которые
дают возможность формирования стабильных структурных систем, распределение
потенциала поля описывает полистепенная суммирована функция, то есть, функция
PES (PES - происходит от PolyExponentialSum).Пример такой функции потенциала
поля и напряженности поля вместе с графиком приведен ниже.
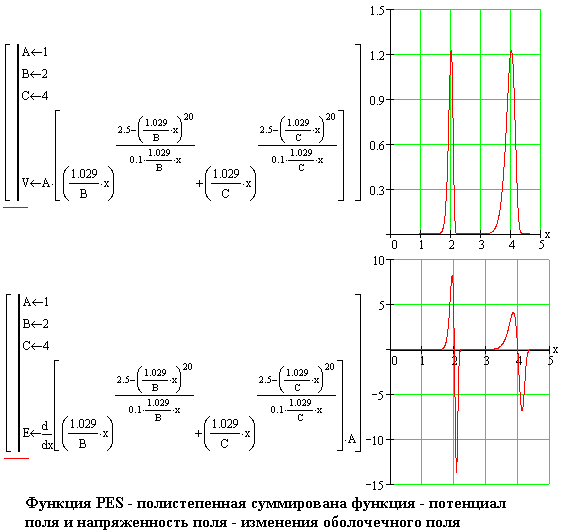
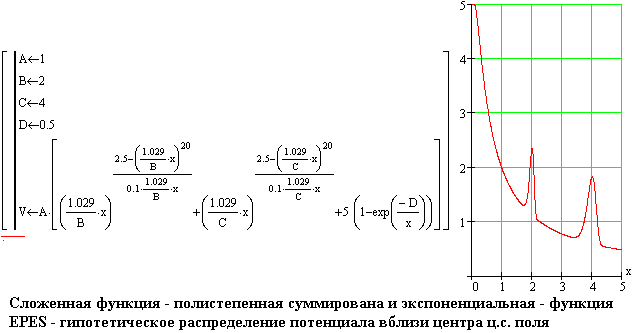
При нано-расстояниях функция PES является одной из двух составляющих
функций. Результирующая функция EPES, которая служит для описания распределения
потенциала вдоль любого луча, который выходит из центральной точки поля,
является суммой двух функций - функции E и функции PES. Потенциал поля,
который описывает функция EPES, и напряженность поля на графике выглядит
следующим образом.
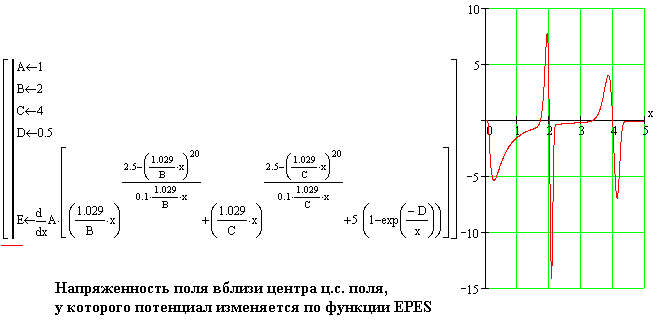
Тот факт, что компоненты вещества обладают сложным распределением потенциала
поля, которое описывается функцией EPES, есть тесно связан с существованием
следующих свойств вещества:
- Вещество в виде скопления, например, в виде планеты, уплотняется
в сторону центра скопления. На такое распределение плотности влияет составляющая
поля, которая описывается функцией Е.
- Вещество существует в виде стабильных структур, например, в виде
атомов, молекул и кристаллов. На формирование стабильных структур влияет
существование потенциальных оболочек с разными радиусами, которые концентрически
расположены вокруг центра поля. Такое распределение поля описывает компонент
PES.
- Когда учитывается существование распределения потенциалов поля фундаментальных
элементов и способ формирования стабильных структур, то это становится
основой для дальнейших интерпретаций физических зависимостей. Исходя из
этого, существование стабильных структур свидетельствует о том, что существуют
два вида структурных компонентов - тяжелые компоненты, известные как нейтроны
и протоны, и легкие компоненты, которые мы знаем как электроны. Основными
строительными блоками вещества являются тяжелые компоненты. Но в случае,
когда они обладали бы большими скоростями, они сами не могли бы успокоить
своего движения и создать стабильные структуры. Легкие компоненты играют
в веществе стабилизирующую роль и успокаивают движение тяжелых компотентов.
А делают это таким способом, что во время формирования стабильных структур
отводят энергию (движения) из этой области наружу.
- Легкие компоненты вещества это те компоненты, которые существуют
прежде, чем из них возникнут электроны - их названо протоэлектронами. Легкие
компоненты заполняют пространство, которое называется физическим вакуумом.
В веществе, которое состоит из атомов, они заполняют пространство между
тяжелыми компонентами, а в частности, они заполняют промежутки между последующими
оболочками и области оболочек. Плотность распределения легких компотентов
(протоэлектронов) в этих структурных системах (нейтронах, атомах, молекулах)
растет таким же образом и по той же причине, как плотность вещества планеты.
- Нейтроны, атомы, молекулы, как стабильные структуры, существуют в
виде стабильного скелета, состоящего из тяжелых компонентов, в которого
объёме сосуществуют легкие компоненты. Благодаря потенциальным оболочкам
тяжелых компонентов, легкие компоненты делятся на секторы, в которых они
заключены и удерживаются с большей или меньшей силой. Одни секторы более
устойчивы к ударам, то есть, они в большей степени стабильны, а другие
в меньшей. Во время столкновения и внезапного изменения направления движения
такой структурной системы (атома, молекулы) некоторые секторы опорожняются.
Потому что находящиеся там протоэлектроны не придерживаются достаточно
сильно, чтобы могли следовать вместе со структурой, успевая за изменением
направления движения. Отрывающееся от структуры облако протоэлектронов
отождествляется с электроном.
Для изучения свойств и описания поведения вещества полезны математические
функции, которые отображают характеристики вещества только приблизительным
способом. Примером может служить функция Ньютона, которая связана с гравитацией.
На протяжении многих лет пользуются нею физики и астрономы, хотя она гравитацию
описывает приблизительно. Иная функция, которая годится для отображения
общих свойств вещества, это полистепенная функция - функция PE. Ниже представлены
графики, на которых показаны примерный потенциал поля, описанный при помощи
функции PE, и напряжённость поля.
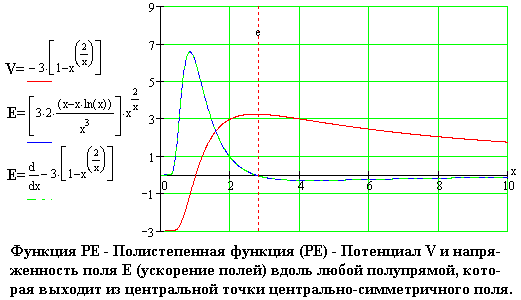
Существование экстремума функции, описывающей потенциал поля, свидетельствует
о том, что из частиц вещества, если они имели бы такое распределение потенциала
вдоль любого радиуса, могли бы формироваться стабильные структурные системы.
А при увеличении расстояния х (на больших расстояниях от начала координат)
значение функции PE, напродобие значения функции Ньютона и функции Е, стремится
к нулю. Такое сходство между этими функциями, особенно сходство между функциями
EPES и PE, которое связано с возможностью создания моделей стабильных структур
вещества и их описания, является достаточным для того, что эти функции
подходят для описания и моделирования различных физических явлений. Особенно
важным является то, что они подходят для описания и моделирования явлений:
электростатических, магнитных, электромагнитных, электродинамических, гидравлических,
аэродинамических, для описания и моделирования движения небесных тел в
космосе и в планетных системах. Такие математические функции особенно полезны
для учебных целей.
Д) Абсолютное и относительное взаимное проницание компонентов вещества
Наличие потенциальных оболочек в пространственном распределении поля,
которое здесь отождествляется с фундаментальным элементом вещества, с одной
стороны, позволяет на формирование и существование стабильных структур
вещества, а с другой стороны, является причиной таких свойств вещества,
как: упругость, сжимаемость, способность к перенесению в веществе структурных
деформаций в виде различных видов волн, и причиной всех других свойств
вещества. Одним из наиболее важных свойства фундаментальных элементов вещества
есть их абсолютная проницаемость. Эту абсолютную проницаемость надо понимать
как одновременное существование всех компонентов вещества в одном и том
же пространстве в виде взаимопроникающихся фундаментальных полей. Эти компоненты,
сосуществуя, одновременно воздействуют друг с другом и взаимно себя ускоряют
- каждый элемент ускоряет все другие элементы в соответствии с тем, какое
есть его распределение напряжённости поля. Абсолютная проницаемость полностью
независима от чего-либо другого и существует в каждый момент времени.
Существует также важное свойство вещества в виде относительной проницаемости.
Но эта проницаемость принадлежит к совсем другой категории. Относительная
проницаемость проявляет себя в том, что данная фундаментальная частица
вещества или сложная вещественная структура в определенной степени теряет
способность воздействия на окружающую среду и сама частично перестает реагировать
на воздействия компонентов окружающего вещества. Относительная проницаемость
появляется в веществе по причине достаточно большой скоростии одних компонентов
вещества относительно других компонентов. Относительная проницаемость связано
в частности с наличием потенциальных оболочек. Потому что, особенно в областях,
где есть расположены эти оболочки, существует большая изменчивость напряженности
поля, то есть, также существует большая способность ускорять другие частицы,
которые появятся в этих областях. Таким образом, даже при относительно
низкой относительной скорости частицы могут стать друг для друга мало заметны.
По той причине нейтрино могут проникать далеко в глубину Земли, и даже
проникать сквозь её тело и лететь дальше в космос.
По причине существования явления относительной проницаемости одно тело,
пролетая на таком же расстоянии возле Солнца может двигаться по параболической
траектории. Другое тело, двигаясь на том же расстоянии от Солнца (в момент
самого большого приближения к Солнцу), но с гораздо большей скоростью,
будет двигаться по гиперболической траектории. Но когда скорость тела,
движущегося вблизи Солнца, будет во много раз больше, то тело тоже будет
двигаться по гиперболической траектории, но она будет иметь едва заметную
кривизну. То есть, говоря другими словами, Солнце будет влиять на тело
(и наоборот, тело будет влиять на Солнце) едва заметным способом.
Явление относительной проницаемости непосредственно связано с явлением
мнимого увеличения массы, которое отчётливым образом проявляется в работе
акселераторов частиц. Большая и всё более увеличивающаяся скорость частиц
в акселераторе является причиной того, что ускоряющие устройства акселератора
во время ускорения частиц оказыват на эти частицы все меньшее влияние.
Поэтому при увеличивающихся скоростях частиц для их последующего ускорения
надо использовать непропорционально больше энергии, а результат в виде
увеличения скорости все более меньший.
Относительная проницаемость вещества была описана в 2006 г. как закон
ничтожного действия - статья об этом законе находится на http://konstr-teoriapola.narod.ru/05_ZakonND.html.
Относительная проницаемость вещества известна тоже как эффект Ушеренко.
А взаимное проникание вещественных структур при больших относительных скоростях
(в виде проникания микрочастиц в тело объекта) имеет большое значение для
прочности и безопасности космических аппаратов.
Е) Принцип минимализации потенциалов пространства
В соответствии с законом свободного падения тел все тела независимо
от их массы в гравитационном поле падают с одинаковыми ускорениями. Обычно
закон свободного падения тел рассматривается в связи с падением небольших
тел на какое-то массивное тело. Но в природе он охватывает разные ситуации
ускорения и падения небесных тел, следовательно, он охватывает также падение
Луны на Землю и Земли на Луну, падение системы Земля-Луна на Солнце и Солнца
на систему Земля-Луна итд. Падение тел в таких случаях происходит лишь
в небольшой степени, ибо только в границах параметров их орбитального движения.
Но взаимное гравитационное ускорение этих тел происходит беспрерывно и
благодаря этому может возникать их орбитальное движение.
Гравитационный закон Галилея касается как небесных тел, так и самых
маленьких тел. А можно его также применять тогда, когда нужно рассматривать
воздействие друг с другом фундаментальных элементов вещества. В такой ситуации
гравитационный закон Галилея становится фундаментальным принципом воздействия
в веществе. Потому что физический принцип воздействия есть один и тот же,
когда воздействие происходит между двумя фундаментальными элементами и
когда воздействие происходит мужду двумя телами, которые построены из фундаментальных
элементов. Тот сам физический принцип работает как между очень отстоящими
друг от друга объектами, так и между объектами при малых расстояниях между
ними, по самые ничтожные расстояния.
Причина движения ц.с. полей выявляет себя, когда анализировать изменения
результирующего потенциала, какие происходят в пространстве в то время,
когда ц.с. поля воздействуют друг с другом и взаимно ускоряют. Причиной
движения является действие пространства, которое заключается на ускорении
находящихся в нём центрально симметричных полей таким способом, чтобы происходила
минимализация (уменьшение) происходящих от этих ц.с. полей результирующих
потенциалов. Отсюда действие пространства можно определить коротко как
действие принципа (М)инимализации (П)отенциалов (П)ространства (в домысле,
гравитационных потенциалов, фундаментальных потенциалов), то есть действие
принципа МПП.
Принцип МПП касается того самого явления, которое описывает закон свободного
падения тел в гравитационном поле. Но с новой точки зрения явление взаимного
воздействия тел, частиц либо ц.с. полей, рассматриваетя глобальным образом
как следствие действия принципа МПП. С той точки зрения это не центрально
симметричные поля, не частицы, не небесные тела "знают", каким способом
они должны ускорять и двигать другие ц.с. поля, частицы и небесные поля.
С той точки зрения ускорением и движением ц.с. полей, частиц и небесных
тел управляет пространство, в котором они вмещаются.
Принцип МПП функционирует в физическом пространстве, в котором каждый
компонент вещества в каждый момент воздействует со всеми остальными компонентами.
Поэтому последствия реализации принципа МПП могут быть анализированы только
при помощи монотонной составляющей математической функции EPES, то есть,
без участия составляющей математической функции PES. Потому что потенциальные
оболочки ц.с. полей, которые описываются функцией PES, касаются воздействий,
которых радиус действия ограничен.
Принцип МПП более подробно представляется на страницы http://konstr-teoriapola.narod.ru/17_PrintsipMPP.html.
Ж) Динамика самодейственного движения вещества
Ньютон, исследуя гравитационные воздействия и свойства вещества, принял
молчаливое предположение. Он предполагал, что в гравитационных воздействиях
тела ускоряют друг друга одинаковым образом в том смысле, что упуская коэффициент
пропорциональности остальная часть математической функции, которая описывает
изменения ускорения тел в зависимисти от расстояния, для всех тел есть
одинаковая. Существование такого предположения видно в третьем законе динамики,
когда рассматривать действие этого закона для случая двух тел, которые
орбитируют вокруг общего центра массы. Равенство сил, которыми эти два
тела воздействуют друг на друга, зависит именно от того, что тела ускоряют
друг друга, а функции, которые описывают эти ускорения, имеют одну и ту
же математическую структуру. В таком случае и силы есть равны, и общий
центр массы остается неподвижен.
Сейчас уже известно, что формула Ньютона описывает гравитационное воздействие
лишь приблизительно. Об этом факте свидетельствует существование движения
перигелия планет и двойных звезд. Орбитальное движение этих объектов можно
описывать более точно при помощи функции, которая является производной
от экспоненциальной функции Е, то есть, при помощи функции 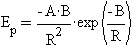 .
Но эта функция одновременно является символическим выражением индивидуального
характера гравитационного поля каждой планеты или звезды. Это значит, что
коэффициенты В в функциях, которые описывают ускорения двух разных объектов,
могут быть разные. В такой ситуации в системе тел не работает динамика
Ньютона, но динамика самодейственного движения вещества. В системе таких
орбитирующих тел динамика самодейственного движения физически выражает
себя таким способом, что тела орбитируют и одновременно такая система как
целое передвигается в пространстве.
.
Но эта функция одновременно является символическим выражением индивидуального
характера гравитационного поля каждой планеты или звезды. Это значит, что
коэффициенты В в функциях, которые описывают ускорения двух разных объектов,
могут быть разные. В такой ситуации в системе тел не работает динамика
Ньютона, но динамика самодейственного движения вещества. В системе таких
орбитирующих тел динамика самодейственного движения физически выражает
себя таким способом, что тела орбитируют и одновременно такая система как
целое передвигается в пространстве.
Подтверждение на основе наблюдатедьных данных существования самодейственного
движения, например, орбитирующей системы двух звезд будет необычно трудным
делом (если вообще это будет возможно). Потому что движение двойной звезды
как целого может быть результатом асимметрии при взаимном ускорении компонентов
двойной звезды (асимметрии, возникшей вследствие различных математических
функций, а конкретно, вследствие того, что 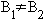 ),
а может быть результатом влияния на систему наружного фактора.
),
а может быть результатом влияния на систему наружного фактора.
Поведение системы в виде двойной звезды можно проследить на модели при
помощи компьютерной моделирующей программы Gas2n-Merkury.*) Ниже показаны
изменения расположения компонентов (модели) двойной звезды в системе координат
X-Z, которые происходят из трех различных ситуаций. Копии образов из экрана
компьютера, которые представляют эти ситуации, были наложены друг на друга,
чтобы показать изменения при различных параметрах.
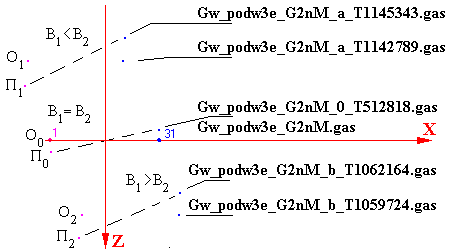 Итак, в самом начале наблюдения процесса компоненты двойной звезды (обозначены
как 1 и 31) находятся в положении
Итак, в самом начале наблюдения процесса компоненты двойной звезды (обозначены
как 1 и 31) находятся в положении 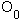 .
Функции их ускорения имеют одинаковые экспоненциальные коэффициенты:
.
Функции их ускорения имеют одинаковые экспоненциальные коэффициенты: 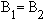 .
В начале наблюдения система находится в положении, когда её компоненты
находятся в апоастер (или иначе, они наиболее отдалены друг от друга) и
лежат на оси Х. Звезды орбитируют в плоскости рисунка таким способом, что
их центр массы находится в начале системы координат. После некоторого времени
расположение центра массы остается без изменений, но изменяется расположение
линии, какая соединяет компонениты, когда они находятся в апоастер.
.
В начале наблюдения система находится в положении, когда её компоненты
находятся в апоастер (или иначе, они наиболее отдалены друг от друга) и
лежат на оси Х. Звезды орбитируют в плоскости рисунка таким способом, что
их центр массы находится в начале системы координат. После некоторого времени
расположение центра массы остается без изменений, но изменяется расположение
линии, какая соединяет компонениты, когда они находятся в апоастер.
На схеме это расположение обозначено как 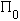 (пи ноль). Моделированная ситуация изменяется, когда при тех же начальных
параметрах системы двойной звезды коэффициенты В для ускорительных функций
обоих звезд из системы различаются друг от друга. Тогда центр массы передвигается.
В зависимости от того, который коэффициент больше, а который меньше, после
некоторого времени звезды расположены в системе координат в местах, которые
обозначены как
(пи ноль). Моделированная ситуация изменяется, когда при тех же начальных
параметрах системы двойной звезды коэффициенты В для ускорительных функций
обоих звезд из системы различаются друг от друга. Тогда центр массы передвигается.
В зависимости от того, который коэффициент больше, а который меньше, после
некоторого времени звезды расположены в системе координат в местах, которые
обозначены как 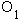 и
и 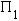 или
или 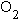 и
и 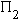 .
.
Пример с самодейственным движением двойной звезды противоречит тому,
что говорит сегодняшняя теоретическая физика. Потому что в выше представленном
примере существует движение общего центра масс двух звезд, которое происходит
по причине их взаимного воздействия друг на друга. Но это не вытекает из
каких-то особенных свойств вещества. Это является следствием известного
поведения вещества, которое заключается в том, что ускорение вещества всегда
происходит в направление увеличения гравитационного (или фундаментального)
поля, которое связано с соседним веществом. Но это также происходит по
той причине, что поле, которое есть связано с разными компонентами вещества,
не изменяется одинаковым образом. Иначе говоря, разные компоненты вещества
прибавляют другим компонентам вещества ускорения, которые изменяются различным
образом.
Описанное поведение вещества и его компонентов можно проследить используя
понятие потенциальных оболочек, благодаря которым существуют стабильные
вещественные структуры.
Две идентичные частицы, из которых каждая находится в области потенциальной
оболочки своей соседки, создают стабильную систему. Расположение частицы
в потенциальном поле соседки схематически выглядит как ниже на рисунке.**)
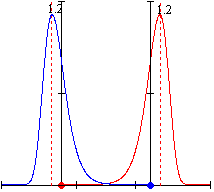 Частицы взаимно ускоряют друг друга и колеблются. Но они постоянно ускоряются
в направление, где находится максимальный потенциал. Во время движения
в каждый момент частицы есть одинаково отдалены от места, где находится
максимум функции, которая описывает потенциал соседней частицы. В каждый
момент, когда одна частица ускоряется "влево", другая частица идентичным
образом ускоряется "вправо". Такое происходит именно потому, что частицы
есть одинаковые - радиус потенциальной оболочки в случае обоих частиц равен
1,2 единиц длины. Если колебательное движение частиц было бы приторможено,
тогда они задержались бы на таком расстоянии друг от друга, что нашлись
бы в местах с самым большим потенциалом, где ускорение равно ноль.
Частицы взаимно ускоряют друг друга и колеблются. Но они постоянно ускоряются
в направление, где находится максимальный потенциал. Во время движения
в каждый момент частицы есть одинаково отдалены от места, где находится
максимум функции, которая описывает потенциал соседней частицы. В каждый
момент, когда одна частица ускоряется "влево", другая частица идентичным
образом ускоряется "вправо". Такое происходит именно потому, что частицы
есть одинаковые - радиус потенциальной оболочки в случае обоих частиц равен
1,2 единиц длины. Если колебательное движение частиц было бы приторможено,
тогда они задержались бы на таком расстоянии друг от друга, что нашлись
бы в местах с самым большим потенциалом, где ускорение равно ноль.
Ситуация будет совсем другая, если в этой системе двух частиц заменить
одну частицу на такую, в которой радиус потенциальной оболочки будет равен
1,1 единиц длины. Схема этой новой ситуации показана ниже.
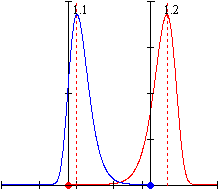 В этой ситуации частицы также могут колебаться друг относительно друга
и также можно их притормозить. Но в этой ситуации они не будут располагаться
в местах с самым большим потенциалом в поле своей соседки. Потому что тогда,
когда одна из них находится в месте расположения потенциального максимума
поля соседки - пусть будет так, что "красная" частица находится на расстоянии
1,1 ед. дл. от "голубой" частицы - то тогда "голубая" частица находится
на "левом склоне" потенциальной оболочки "красной" частицы и на неё действует
ускорение, которое есть направлено "вправо". Следовательно, эта частица
будет удаляться от "красной" частицы и "красная" частица тоже окажется
на "левом склоне" потенциальной оболочки "голубой" частицы. В случае приторможения
взаимных колебаний обоих частиц обе эти частицы будут расположены на "левых
склонах", в местах с одинаковыми наклонениями склонов. Иначе говоря, обе
частицы будут иметь приблизительно одинаковые ускорения "вправо". Такое
произойдёт, когда расстояние между ними будет равно около 1,10448 ед. дл.
После наложения друг на друга графики напряженности поля обоих частиц представлены
ниже.
В этой ситуации частицы также могут колебаться друг относительно друга
и также можно их притормозить. Но в этой ситуации они не будут располагаться
в местах с самым большим потенциалом в поле своей соседки. Потому что тогда,
когда одна из них находится в месте расположения потенциального максимума
поля соседки - пусть будет так, что "красная" частица находится на расстоянии
1,1 ед. дл. от "голубой" частицы - то тогда "голубая" частица находится
на "левом склоне" потенциальной оболочки "красной" частицы и на неё действует
ускорение, которое есть направлено "вправо". Следовательно, эта частица
будет удаляться от "красной" частицы и "красная" частица тоже окажется
на "левом склоне" потенциальной оболочки "голубой" частицы. В случае приторможения
взаимных колебаний обоих частиц обе эти частицы будут расположены на "левых
склонах", в местах с одинаковыми наклонениями склонов. Иначе говоря, обе
частицы будут иметь приблизительно одинаковые ускорения "вправо". Такое
произойдёт, когда расстояние между ними будет равно около 1,10448 ед. дл.
После наложения друг на друга графики напряженности поля обоих частиц представлены
ниже.
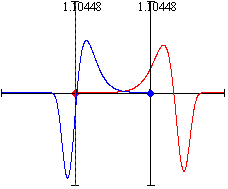 Больше подробностей видно на ниже приведенных графиках.
Больше подробностей видно на ниже приведенных графиках.
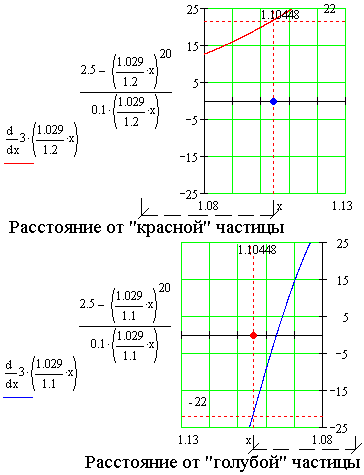 На схеме, на которой частицы находятся на фоне графика напряженности поля
своей соседки, можно увидеть следующий образ. "Голубая" частица находится
в области положительной напряженности поля "красной" частицы, следовательно,
она ускоряется в направление увеличения расстояния от "красной" частицы,
то есть, вправо.
На схеме, на которой частицы находятся на фоне графика напряженности поля
своей соседки, можно увидеть следующий образ. "Голубая" частица находится
в области положительной напряженности поля "красной" частицы, следовательно,
она ускоряется в направление увеличения расстояния от "красной" частицы,
то есть, вправо.
"Красная" частица находится в области отрицательной напряженности поля
"голубой" частицы, следовательно, она ускоряется в направление уменьшения
расстояния от "голубой" частицы, то есть, она тоже ускоряется вправо
З) Самодейственное движение вещества в свете опытных фактов
Самодейственное движение вещества можно рассматривать в двух различных
контекстах. В одном контексте самодейственное движение вещества существует
в том смысле, что компоненты вещества (например, атомы) движутся относительно
друг друга. Это происходит вследствие взаимного ускорения. Но эта система
атомов и её общий центр массы не меняет своего положения и в никакое направление
не ускоряется. Так ведёт себя, например, молекула газа, то есть, структурная
система, которую создают два одинаковых атома газа.
До сих пор ещё никто не исследовал атомов под углом их ускоряющих способностей.
Потому функции, которые описывают их напряженность поля, ещё неизвестны.
Следовательно, пока что по необходимости нужно пользоваться гипотетическими
моделями полей и частиц, а также структурными системами, какие при их помощи
можно создавать.
Вот наиболее простой пример такой системы - она состоит из двух частиц
и её начальные параметры записаны в рабочем файле DC_1.2-1.2.gas.**) После
ознакомления с упражнением, которое можно провести с этим файлом при помощи
компьютерной программы Gas2n.exe, можно заметить, что неподвижность центра
массы этой системы двух частиц связана с тем фактом, что математические
функции, описывающие ускорения, которые каждая из этих частиц прибавляет
второй частицы, есть идентичны, а прежде всего идентичны есть значения
экспоненциального коэффициента В в этих функциях - они равны 1,2.
Совсем другие есть свойства системы двух частиц, в которой значения
экспоненциального коэффициента В для обоих функций есть разные. Тогда существует
самодейственное движение вещества, которое надо понимать совсем по-другому.
Тогда существует взаимное ускорение частиц, как и в предыдущем случае,
но существует тоже вид асимметрии в процессе взаимного ускорения частиц.
В результате возникает результирующее ускоренное движение системы частиц.
Упражнение с такой системой частиц можно провести пользуясь рабочим файлом
DC_1.2-1.1.gas.
После включения процесса, которого начальные параметры есть записаны
в рабочем файле DPC_1.2-1.1a.gas, можно увидеть соединенные друг с другом
две пары частиц. Каждая пара (когда она находится в отдельности) самодейственно
ускоряется, а эти ускорения имеют противоположные направления. Однако соединенные
с собой две пары частиц не удаляются друг от друга, ибо целую систему в
стабильном положении придерживают две центральные частицы - „зелёные” частицы.
Это есть пример стабильной системы, которой центр массы остается неподвижен,
несмотря на то, что компоненты этой системы (в виде пар частиц) обладают
тенденцией к самодейственному ускоренному движению. В этом случае стабильность
системы четырех частиц есть устойчива. Это значит, что несмотря на наличие
небольшого колебания компонентов системы вокруг положений равновесия***)
и существования тенденции пар частиц к самодейственному ускоренному движению,
амплитуды колебаний частиц и их энергия не увеличиваются, а следовательно,
система частиц не разрывается.
Эта система устойчива даже после истечения времени, в которое будет
выполнено свыше сто тысяч вычислительных итераций - состояние такой системы
записано в файле DPC_1.2-1.1a_T100079.gas. Чтобы время, которое в этом
процессе истекает, сделать более реальным и иметь для него сравнительную
единицу, можно его сравнить с количеством вычислительных итераций, которые
отвечают одному периоду колебания частицы, которая находится в этой системе.
Одному периоду колебания частицы отвечает приблизительно около 200 итераций.
Совсем по-другому ведёт себя другая система, которая состоит из тех
же четырех частиц, но её центральными частицами есть две „жёлтые” частицы.
Начальные параметры этой системы есть записаны в рабочем файле DPC_1.2-1.1b.gas.
Эта система также является стабильной системой, но процесс сохранения стабильного
состояния должен проходить в других условиях. А именно, она будет стабильной
только тогда, если после включения процесса активной будет кнопка "Cooler".
Тогда увеличение энергии, которое происходит в этой системе, будет из системы
отведено наружу. Если наблюдать за поведением этой системы без включения
кнопки "Cooler", тогда система не сохраняется в целом даже в то время,
которое отвечает 5000 вычислительных итераций. Такая система частиц, уже
рассыпающаяся, есть записана в рабочем файле DPC_1.2-1.1b_T4717.gas.
Наблюдая за процессом, которого начальные параметры есть записаны в
файле pliku DPC_1.2-1.1b_T4717.gas, можно наблюдать два явления, которые
есть связаны с системой частиц - с той, которая ещё недавно существовала
как целое, и с отдельными парами частиц, которые соединялись друг с другом.
После включения процесса пары частиц в начале процесса летят в противоположные
стороны, а частицы видимым образом колеблются. После включения при помощи
кнопки "Cooler" процесса торможения движущихся частиц доходит до задержки
ускоренного движения частиц, а после этого начинается ускоренное движение
в противоположное направление. Таким образом выявляется факт, что с функциями,
которые описывают ускорения частиц, связано существование двух разных направлений,
в которые эти пары частиц могут самодейственно ускоряться. Ускорение в
одно направление - то ускорение, которое существовало в начале процесса,
когда частицы сильно колебались - можно относительно легко затормозить
и элиминировать. Когда это наступает, начинается процесс ускорения в противоположное
направление, несмотря на существование тормозящего воздействия, которое
включилось кнопкой "Cooler".
Второе явление связано с различной устойчивостью систем, возникающих
из двух представленных пар частиц, в двух ситуациях: 1) когда эти пары
соединяются с собой в одну систему при помощи „залёных” частиц и 2) когда
соединяются с собой при помощи „жёлтых” частиц. Чтобы это различие увидеть,
надо включить процесс, которого начальные параметры есть записаны в файле
DPC_1.2-1.1b_T4717.gas. Не ожидая слишком долго, чтобы пары частиц слишком
не ускорились и не исчезли из поля экрана, надо при помощи кнопки "Cooler"
включить торможение частиц. После включения торможения пары частиц в начале
задерживаются, а потом начинают ускоряться "к себе". Кнопка "Cooler" всё
время должна быть активной. Пары частиц будут приближаться друг к другу,
аж в некий момент "жёлтые" частицы найдутся на таком расстоянии, на котором
они находятся, когда участвуют в создании стабильной системы. Но до задержки
движения частиц не дойдёт и не возникнет стабильная система. (Можно догадываться,
что для того, чтобы это могло произойти, торможение частиц должно быть
более сильным.) Пары частиц будут двигаться дальше, аж до того момента,
когда на подобном расстоянии друг относительно друга найдутся "зелёные"
частицы. Только тогда прекрарится ускоренное движение пар частиц и возникнет
стабильная система четырех частиц.
Поведение представленных здесь самоускоряющихся пар частиц это пример
поведения самой простой системы. Самоускоряющиеся структурные системы могут
состоять из большого количества частиц, но их поведение будет подобное.
При некоторых взаимных расположениях их результирующие ускорения могут
иметь
одно и то же направление, а тогда они будут стремиться друг возле друга
в то же направление. В подходящих условиях такие частицы могут связываться
друг с другом уже известным способом и создавать большую стабильную самоускоряющуюся
частицу. Те же самые частицы в других расположениях друг относительно друга
будут обладать противоположными направлениями самоускорения, а в соединении
с собой создадут стабильную частицу, которая не будет обладать способностью
самоускорения.
Самоускоряемые частицы, в виде сложных систем частиц, я здесь буду попеременно
называть также частицами-баронами. Потому что частицы-бароны напоминают
эпизод с жизни барона Мюнхаузена, который сам себя, вместе с лошадью, которую
сжимал между коленами, за волосы с глубокого болота вытащил. Частицы-бароны
необычно трудно увидеть в физических явлениях, а эта трудность вытекает
по одной причине. Чтобы в веществе увидеть частицы, которые похожи на частицы-бароны,
нужно чтобы в уме тлелось хотя бы слабое подозрение, что такие частицы
вообще в природе могут существовать. Если „заранее” сказать, что в природе
нет никаких указаний, подсказок, ни доказательств того, что частицы-бароны
существуют, то тогда их способности и приметы не имеют права существовать
в интерпретациях физических явлений.
Тогда всякие явления, которые простым способом можно бы выяснять при
помощи свойств частиц-баронов, а прежде всего путем дифференциации ускорительных
функций, обязательно должны выясняться другим способом или вообще не иметь
никакого выяснения.
Существование частиц-баронов вытекает с опытных фактов, следовательно,
эти факты должны быть представлены. Ибо они свидетельствуют о том, что
конструктивная теория поля не противоречит опытным фактам и правильно описывает
мир физических явлений. Вот несколко таких опытных фактов.
Факт 1. Радиоактивность химических элементов в виде распада атомов является
следствием расшатывания стабильности структуры атомов. Сам процесс распада
атомов является побегом из их структуры компонентов - частиц-баронов. Такой
частицей-бароном является частица альфа, или иначе, соединенные друг с
другом два протона и два нейтрона. На ускорительные свойства частицы альфа
влияет тот факт, что нейтрон и протон ускоряют друг друга по различным
функциям. Но это не единственная разница. Ибо существуют ещё такие последствия,
что протон как тажёлый компонент вещества (о тяжёлых и лёгких компонентах
вещества я упоминаю в точке Г) относительно легко теряет часть своего протоэлектронного
облака, которая (эта часть) отождествляется с электроном. А нейтрон, как
соединение тяжёлого компонента (которому я здесь не даю отдельного названия)
и окружающего его и проникающего облака протоэлектронов, сильно держит
это облако в области своих потенциальных оболочек. Соединение друг с другом
в соответствующей структурной системе двух разных тяжёлых компонентов,
нейтронов и протонов - даже если протоны будут окружены облаками протоэлектронов,
в которых не будет никаких убытков, а наружу такие структуры будут себя
проявлять как неионизированные атомы - когда оно находится в структуре
тяжёлого атома, является постоянной, потенцаильной причиной распада этого
тяжёлого атома. Расшатание равновесия в такой структурной системе может
стать причиной отсоединения от целого частицы-барона. Тогда со свойственным
ей самоускорением она убегает. Именно такое происходит в случае радиоактивного
распада, во время которого происходит эмиссия частиц альфа.
Факт 2. Существование асимметрии в ускорениях протонов и нейтронов является
также причиной движения частиц бета. Во время ядерных процессов, в виде
распада и реорганизации структуры, разница в ускоряющем воздействии тяжёлых
компонентов атомных ядер проявляет себя также в виде результирующего ускорения
лёгких компонентов, то есть, электронов. С точки зрения причинности этот
процесс есть идентичный с контактным явлением в виде течения электрического
тока и возникновения электрического потенциала на стыке двух металлов,
например, на стыке Fe-Cu. Но в контактном явлении участвуют потенциальные
оболочки, которых радиусы есть значительно больше и есть другие распределения
потенциалов в области этих оболочек, чем в области оболочек с малыми радиусами.
По той причине в контактном явлении электроны (до момента появления на
электродах максимального значения электрического потенциала) движутся со
значительно меньшими скоростями, чем скорости частиц бета, которые вылетают
во время радиоактивного распада.
Факт 3. В первую очередь я представлю этот факт с теоретической точки
зрения, а позднее представлю его в связи с физическими явлениями в природе.
Используя рабочий файл DPC_1.2-1.1.gas, можно провести два упражнения
с частицами-баронами. В одном упражнении можно наблюдать движение частицы-барона
при активной кнопке "Cooler", когда движение частиц тормозится, а частицы
во время каждой вычислительной итерации теряют 1% своей скорости.
Во втором упражнении можно наблюдать движение частицы-барона, когда
это движение не тормозится. После выполнения упражнений, на основе их результатов
можно увидеть следующее.
- При отсутствии тормозящего фактора частица-барон сохраняет в приближении
постоянное ускорение. Таким образом, после достаточного времени полёта,
она может достичь сколь угодно большую скорость.
- В случае, когда существует тормозящий фактор, частица-барон передвигается
ускоренным движением только в течение короткого времени в начале процесса.
Отведение появляющейся надбавки энергии приводит к тому, что ускоренное
движение останавливается, а частица-барон дальше движется поступательно
с некоторой определённой скоростью.
Представленные зависимости видны в результатах, которые происходят
из нескольких примерных упражнений - они записаны ниже.
 В рабочих файлах DC_1.2-1.1_T10001_Cr.gas и DC_1.2-1.1_T20002_Cr.gas есть
записаны параметры одного компонента из частицы-барона - "зелёной" частицы
(после 10001 и после 20002 вычислительных итераций). Процесс проходил с
одновременным торможением движения частицы-барона. Видно, что после 10001
вычислительных итераций и после 20002 итераций скорость есть одна и та
же. То есть, это значит, что когда от частицы-барона отнимать энергию,
то при некоторой скорости это отнятие энергии равновесит увеличение энергии
(которое связано с ускорением частицы) и скорость частицы не увеличивается.
В рабочих файлах DC_1.2-1.1_T10001_Cr.gas и DC_1.2-1.1_T20002_Cr.gas есть
записаны параметры одного компонента из частицы-барона - "зелёной" частицы
(после 10001 и после 20002 вычислительных итераций). Процесс проходил с
одновременным торможением движения частицы-барона. Видно, что после 10001
вычислительных итераций и после 20002 итераций скорость есть одна и та
же. То есть, это значит, что когда от частицы-барона отнимать энергию,
то при некоторой скорости это отнятие энергии равновесит увеличение энергии
(которое связано с ускорением частицы) и скорость частицы не увеличивается.
В двух остальных файлах есть записаны параметры "зелёной" частицы после
подобного течения процесса, но при отсутствии торможения частицы-барона.
В этом случае видно, что ускоренное движение после двукратно большего времени
привело к тому, что скорость частицы-барона увеличилась двукратно. Такое
происходит в случае равноускоренного движения.
В природе существуют различные частицы, которые мчатся с разными скоростями.
На тему причин скорости частиц могут существовать различные догадки. Можно
связывать с ними причины, которые действуют коротко и ускоряют их, прибавляя
огромные скорости в самом начале их движения, и можно догадываться, что
это есть частицы-бароны, а причина движения каждой такой частицы-барона
связана непосредственно с нею самой и является её физической приметой.
Есть основания для того, чтобы полагать, что в природе существуют обе причины
движения.
Причиной выброса частиц из материальных структур, которые во время
движения ведут себя в соответствии с законами динамики Ньютона, есть кратковременное
ускоренное движение. Этот начальный этап движения частиц возникает в структуре
в тех областях, где существуют потенциальные оболочки. Частицы, создавая
структурные системы, на таких расстояниях наиболее энергично воздействуют
друг с другом и тогда прибавляемые ими ускорения есть самые большие. При
подходящих расположениях частиц друг относительно друга могут возникать
большие результирующие ускорения, которые дуйствуя на (другие) частицы
в короткое время действия прибавляют им большие скорости. И именно в связи
с возможностями ускорения и условиями, в каких потом движутся ускоренные
частицы, можно предполагать, с какими скоростями могут перемещаться одни
и другие частицы.
Существование в физическом вакууме материальной среды в виде протоэлектронной
атмосферы, с одной стороны, делает возможным распространение разновидных
волн, часть из которых мы воспринимаем как световые волны, а с другой стороны,
является причиной торможения движения частиц, которые в этой среде движутся
с большими скоростями. Отсюда можно принять заключение, что частицы, которые
мчатся в космосе с околосветовыми скоростями, не могли быть ускоренны до
столь огромных скоростей во время короткого акта ускорения, например, во
время ядерного взрыва. Эти частицы характеризуются приметами частиц-баронов.
Потому что частицы, которые ускоряются во время короткого процесса, даже
если они приобретают большие скорости, вследствие тормозящего воздействия
среды, в которой они движутся, уменьшают скорость до всё более меньших
значений. А только частицы-бароны могут ускоряться теоретически до сколь
угодно большой скорости. Но практически, по причине тормозящего воздействия
протоэлектронной среды, какая существует в физическом вакууме, скорость
частиц-баронов есть ограничена именно вследствие сопротивления среды.
Рассуждая теоретически, в разных местах пространства протоэлектронная
среда имеет разновидную плотность. В физическом вакууме, в областях, которые
очень отдалены от больших скоплений вещества, эта среда есть наименее плотная.
Поэтому может случиться такое, что в такой области частицы-бароны вследствие
самоускорения приобретут столь большие скорости, что благодаря явлению
относительной проницаемости почти исчезнет их взаимное воздействие и влияние
как с протоэлектронами, так и с остальным веществом. Тогда такие частицы-бароны
есть в некотором смысле потеряны для нашего материального мира. Ибо они
будут дальше ускоряться и приобретать всё большие скорости и уже никогда
и никаким способом их невозможно будет наблюдать.
Движение частиц-баронов можно было бы заметить на основе одной особенной
приметы. Если получилось бы наблюдать движение частицы по спиральной траектории,
а при том шаг спирали увеличивался бы, то это была бы информация, что движется
именно частица-барон, которая одновременно очень медленно вращается.
Интерпретации многих других физических явлений можно найти в статьях
на http://konstr-teoriapola.narod.ru/index.html.
____________________________________________
*) Внимание: Компьютерные моделируюшие программы, которые можно скачать
на "страницы пинопы", работают правильно на компьютерах с системами Windows
ME i Windows XP.
Чтобы выполнить упражнение с моделью двойной звезды, надо скачать файл
Merkury.zip (http://pinopapliki2.republika.pl/Merkury.zip),
в котором находятся две исполнитьельные программы exe и рабочие файлы gas.
При помощи исполнительной программы Gas2n-Merkury.exe надо открыть папку
файлов "Gwiazda_podwojna", открыть нужный файл в формате gas и включить
течение процесса. В рабочем файле находятся закодированные начальные параметры
процесса: расположение в системе отсчёта и начальная скорость. А изменения
движения объектов во время течения процесса происходят вследствие их взаимного
ускорения. Чтобы на экране наблюдать изменения процесса, надо 12 раз кликнуть
левой клавишей мышки (курсор должен находитюся на пульте моделирующей программы)
на чёрной стрелке, которая направлена «вверх-вправо». Тогда моделируемые
объекты есть видны на экране.
**) Чтобы выполнить упражнение с взаимно ускоряющимися частицами, надо
использовать исполнительную программу Gas2n.exe. После открытия этой программы
надо в таблицы "Formula" сделать активной кнопку "PES". Потому что частицы
воздействуют друг с другом именно в соответствии с этой математической
функцией.
Для торможения движения частиц, то есть, для отведения части энергии,
которая есть связана с текущим процессом, служит кнопка "Cooler". Когда
кнопка "Cooler" активна, тогда при вычислении последующих расположений
частиц в системе отсчёта, во время каждой вычислительной итерации, скорость
частиц уменьшается на 1%.
***) Небольшие колебания вокруг положений равновесия компонентов, которые
на экране кажутся быть расположены неподвижно, можно наблюдать, когда кнопка
"Show Listing" есть активна. Тогда на таблицы "Listng" видны изменяющиеся
скорости частиц или их позиционные параметры. Перемена скорости частиц
на таблицы "Listng" на их позиционные параметры (или перемена в противоположное
направление) получается, когда два раза кликнуть левой клавишей мышки,
при чем курсор должен быть расположен на белом поле таблицы.
При активной кнопке "Show Listing" моделируемый процесс видимым образом
замедляется, что позволяет более точно задерживать в подходящий момент
работу программы, чтобы записывать параметры процесса.
Богдан Шынкарык "Пинопа"
Польша, г. Легница, 2011.07.17.
________________________________
Накопление энергии в структуре материи и ее освобождение
(Комментарий на http://manipulatorzy.salon24.pl/343451,sensacyjna-propozycja
- @ ZEWSII - Чтобы понять, нужно потрудиться ...)
1. Движение в материи существует по той причине, что компоненты, которые
создают структурную систему, прибавляют друг другу ускорения.
2. Когда компоненты (создающие структурную систему) прибавляют друг
другу ускорения и эти ускорения изменяются по одной и той же математической
функции, тогда результирующее ускорение системы равняется ноль и центр
массы системы остается неподвижен.
3. В природе существуют структурные компоненты материи, которые прибавляют
другим компонентам ускорения, изменяющиеся по различным математическим
функциям. Доказательством того, что существуют такие различные ускорительные
функции, есть существование разновидных структур кристаллов, которые образуются
атомами различных химических элементов. Об этом свидетельствуют различные
расстояния между атомами в кристаллах и разные расстояния между атомами
в различных химических соединениях. Если бы все атомы (независимо от вида
химического элемента) ускоряли по одной и той же математической функции,
тогда создаваемые ими структуры всегда имели бы повторяющееся строение.
4. Взаимное ускорение атомов в структурной системе, которое происходит
по различным математическим функциям, вызывает такой результат, что результирующий
центр массы системы не может оставаться неподвижнымным - он должен двигаться
с некоторым результирующим ускорением. Такие автоматически ускоряющиеся
структурные системы - это частицы-бароны.
5. В природе частицы-барони не могут всё время ускоряться и достигать
неограниченные скорости. Это невозможно по причине существования тормозящего
воздействия другого (постороннего) вещества и невозможно даже по причине
существования большого количества самих же этих частиц-баронов. При большом
их количестве и тормозящем воздействии окружающих частиц из них образуются
устойчивые системы (более сложные частицы), которые не способны самостоятельно
ускоряться. Только тогда, когда такая система (не способна самоускоряться)
будет расшатана, её компоненты ускоряются и разлетаются в разные стороны.
Именно таким способом происходит блокировка энергии в структурных системах
материи, а когда происходит расшатывание равновесия систем и их разрушение,
тогда происходит освобождение энергии.
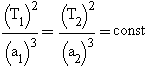 ,
где T с индексом 1 или 2 это периоды обращения двух планет, зато а с индексом
1 или 2 это большие полуоси этих орбит. Эту формулу можно немножко изменить
и для двух планет написать её в виде
,
где T с индексом 1 или 2 это периоды обращения двух планет, зато а с индексом
1 или 2 это большие полуоси этих орбит. Эту формулу можно немножко изменить
и для двух планет написать её в виде 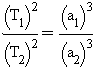 .
Можно ещё перейти к более идеализированной форме планетной системы, в которой
планеты движутся по круговым орбитам. Тогда в формуле вместо отношения
кубов больших полуосей эллиптических орбит выступает отношение кубов радиусов
круговых орбит, а формула имеет вид
.
Можно ещё перейти к более идеализированной форме планетной системы, в которой
планеты движутся по круговым орбитам. Тогда в формуле вместо отношения
кубов больших полуосей эллиптических орбит выступает отношение кубов радиусов
круговых орбит, а формула имеет вид 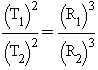 .
.

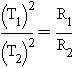 .
.
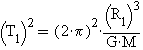 ,
, 









